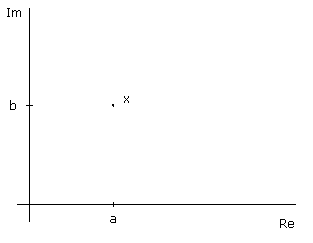Matematica
Lezione 1 (21/2/2001) _________
Lezione 2 (28/2/2001)
________ Lezione
3 (7/3/2001) _________ Lezione 4
(14/3/2001)
Lezione 5 (21/3/2001)
_________ Lezione 6
(28/3/2001) ________ Lezione 7 (4/4/2001)
_________ Lezione 8 (11/4/2001)
Lezione 9 e 10 (2 e 9/5/2001)
___ Lezione 11
(16/5/2001)
________
Lezione 12 e 13 (23-30/5/2001)
________
Lezione 14 (8/6/2001)
Lezione 15 (13/6/2001)
Lezione del 21/2/2001
Ricordare che...
- Si possono usare, nei
calcoli, delle lettere al posto dei numeri: in questo
caso si parla di Calcolo letterale; la lettera indica qualsiasi
numero. Ad esempio, l'espressione algebrica 2a può valere 4 se alla lettera a sostituiamo 2, o 6 se ad a sostituiamo 3.
- Le somme algebriche
vanno calcolate tenendo conto del segno di ogni termine
dell'espressione e del fatto che vale la proprietà
commutativa. Ad es., -5+4 = +4-5 = -1.
- Il il segno
del prodotto fra numeri relativi segue la legge di
composizione dei segni: -*- = +, +*- = -, -*+ = -, +*+ =
+.
Ad es., (-1)(-2) = 2.
- Le
operazioni aritmetiche hanno priorità diverse; in
un'espressione, una moltiplicazione (o una divisione) va
eseguita sempre prima delle somme (o sottrazioni). Ad
es., 2*3+4
= 10
e non 14. Le parentesi, in un'espressione, possono
alterare queste priorità. Ad es., 2*(3+4) = 14 e non 10.
- Se sommiamo
(sottraiamo, moltiplichiamo o dividiamo) ambo i membri
di un'eguaglianza con una stessa quantità, non
modifichiamo la validità dell'eguaglianza stessa. Ad
es., la banale eguaglianza 2 = 2 non cambierà (sarà
sempre verificata) se sommiamo ambo i membri con 3 (2+3 = 2+3 cioè 5 = 5 è sempre
verificata). Altro esempio: a + 3 = 5 non cambierà se
la trasformiamo così: a + 3 - 3 = 5 - 3 (abbiamo
sottratto 3 ad ambo i membri) così come 2a = 4 non cambierà se
la trasformiamo in 2a/2 = 4/2.
- Dal punto
precedente discende la definizione, e il procedimento di
risoluzione, di equazione, cioè qualsiasi
eguaglianza in cui compaiano dei termini noti
e dei termini incogniti; le
equazioni di 1° grado sono quelle in cui il termine
incognito compare alla prima potenza. Ad esempio, x + 1 = 2 è un'equazione
di 1° grado poiché la x, lettera con cui
si indica di solito il termine incognito, è alla potenza
1; per risolvere questa equazione applichiamo i risultati
ottenuti nel punto precedente: sottraendo 1 da ambo i membri
otterremo: x + 1 -1 = 2 - 1 cioè x = 1; come si vede,
si tende a fare in modo di avere tutti i termini con
l'incognita a sinistra del segno di uguaglianza e tutti i
termini noti (i numeri) a destra; il numero a destra del
segno = dell'ultima espressione è la soluzione dell'equazione.
Altro esempio: l'equazione 3x = 9 diventa
(dividendo ambo i membri per 3) 3x/3 = 9/3 cioè x = 3.
- Si può
accelerare il procedimento di risoluzione osservando che
quando scriviamo x + 1 -1 = 2 - 1, come
nell'esempio precedente, è come se dicessimo: un termine
additivo (+ 1 nell'esempio) che compare da un lato del
segno = può essere portato dall'altra parte
cambiato di segno (l'equazione originaria era x + 1 = 2 che, portando + 1 a destra del
segno =, diventa x = 2 - 1 ....). Allo stesso
modo, un termine che in un membro moltiplica, portato
all'altro membro dividerà; ad es., 3x = 9 diventa,
portando il 3 a destra del segno di uguaglianza, x = 9/3.
- Vale, in
un'espressione letterale, la proprietà distributiva;
ad es., 5(a + b) = 5a + 5b, cioè il numero
5, che sta fuori
della parentesi, moltiplica tutti (e soli) i termini
additivi dentro la parentesi.
- Vale anche
l'inverso: si possono raccogliere tutti i termini comuni
presenti in un'espressione e metterli in
evidenza; ad esempio nell'espressione 7x + 7y possiamo mettere
in evidenza il 7, che compare in entrambi i termini,
ottenendo così 7(x + y).
Esercizi (Equazioni di 1° grado)
- x+3(1 -x)
=2+5x.
- 4(1+x) -
3(2-x)=4+3x(1-1/3)
- 3-2(4x-3)
=x-3(2x+5).
- 5(2+x)=3(1+x)-2x-4(2-x).
- (7-3x)2
+ x = 5 - 3(5 -x)
- 2(x-3)-4(1
-2x) =3(x-l).
- 3(x-1)-2x+5=4(x-2)+4.
- 3x2-1-x=x(3x+1}+5.
- 6(x+2)-3(x+4)+3=2x+4(x+1).
- 2(x-3) -5(1
+x) -1 =x+2(1-x);
- (x-1)(x+1)+2(1-3x)=(x+2)(x-3)-3.
- 3-2(x+2)-(1+4x)=x-2(2x+1).
- 3x(x- 1) -
(1 +x) (-4) =2x2 - (1 -x) (1 +x) +4.
- 2-[2x- (3
-x) -4] = (1 -2x)3+2 -3x;
- -2[x(x -
1)-1 +x(3 - x)] = -2(1 +5x) +4.
- x-1+ 5(x -
3) + (-2)2 = 6(x - 2).
Se si hanno problemi a eseguire
le equazioni:
- Svolgere questi
esercizi sulle operazioni tra numeri relativi
Calcolare le seguenti somme
algebriche:
+3-6; -2+5;
2+2; -3-4; +3 +4; -5 +1; 2+3; 1+5; - 2+3; +1,-5; - 2,3; -1,5;
1,8; -0,5; 0,2; -3,4; 1,3; 0+(-3)
(-3)+(-5,8); -4 + (+3,2); -3 + (-1.7); -3 + (+1,7); (-7) + (-7);
1,3+(-0,2).
(+3) + (-2) + (-4); (-1) + (-3) + (-5); (-5)+ (+5)+ (-6); (-4) +
(-1) + (+4).
( 2,5) + (+1,3) + (0,2); (-2,1) + (-1,3) + (+4);
2,3+(-1,.2)+(+1,2); -5+7-8+10; -4+0,5-7,3+9,2.
Moltiplicazioni
(-5+2)(-3);
(-1+4-9 )(+1); (-8)(-7+4+3);
-4(5+2,5-4,5); (-8,3+4,2-0,7)(-2); (-1)(+2)(-6);
(+4)(-2)(+2); 3(-3)(-2); (+5)(-2)(+3);
0,1·(+3)·(-0,4); 0,2 (-3,5)·(+1,2); -2,3(+0,9)·(-0, 5).
- Svolgere le seguenti
espressioni letterali
a-(a+b); a + (2a
-b); a2 - (a - b); (a+b)2 a2+b2;
2(a+b); 2a - a2; (x+y)/2; (a + b)2 - (ab)2.
Calcolare il valore delle seguenti espressioni attribuendo alle
lettere i valori numerici posti a fianco di ciascuna di esse
3a2b;
-2ab3 per a=-2/3;
b=+3/2
(ab-2a-3b+6) / (a2 - 2a -3) per a=-3/5; b=0,2
[(a2
- b2) / (a-b)2][(a2 + ab) /
(a-b)2] per a=3/4
; b=-2/5
Calcolare:
(2a+4b -
6c)(-2b); (7x - 2y)(-3x); -7(10a + 15a - 5); (-3x2 +
6x - 1) (-8/3);
+3x(x2
- 3x 42); -4ab(2a2 +3ab-b2); -4a2b3(a+2a2b-3a3);
(a2 + a + 1)2a3;
(4x2
- 5x)(-2x2); (-2x2)(4x2 - 5x);
(x + 2)(-5x2y); 2a3b2(-2a+b-a2
+2b2);
(-7b+2a) 7a2b2
+ (-a2b)(8a2 +5ab -4b2); (-2a2)(3ab
+5a2- 3b2) - 4a2b(4 - 7a + 8b).
5a2b(2a
- 3b) - (1/2)a2(ab - 4a2 - 2b3)
+ (-2a)4; 8x3 - {(+1/4)x[(x2 - y2)(-2)2
- 4x2]+ 8x3}.
Raccoglimento a fattor comune
Scomporre in fattori le seguenti espressioni mettendo in
evidenza in ciascuna di esse i fattori comuni
a2+4a;
2+6a; a3+a2; a5+8a3;
-x3-2x2-5x.
x2yz
+ 2xy2 z + xyz2; 4mn2 - 6m2n;
(1/9)a3b3 +(2/3) a2b4;
(a+b)x2
+ (a+b)y+2(a+b)x; x2y(x-y) +3x3y(x-y) +4xy2(x-y).
9axy-6a2x;
5m2+ l0m; 4a2b2 -6a3b+8a2b3;
9a3 +3a+3.
15a-20a2+25ab;
x10 -x8 +4x6; 12xy2 -
15xy+ 18x2y; 0,5a3b4 - 1,5ab3.
a3
-4a2 +5a; 6x3 - 12x2y+24x4;
x6y4 -x3y3 +4x4y2
(1/4)a3b2c2+(3/2)a2bc2
- (5/4)a2bc4 + (1/8)a2b2c2
-(5/2)a2b3c3.
2(a-
l)+x(a-1)-2xy(a-1); 3x(a+1)+a+1-8x2(a+1).
(a-b)2+2(a-b)
- (a-b)ab; (x+2y)2 -3(x+2y) +2(x+2y)3.
(3a+1)(2a-3)-4a(2a
-3)-7(2a-3).
(a-1)(a
-2)(a-3)-3(a- 1)(a-2)+(a-1)(a-2)2a+(a-1)(a-2).
a(x-1)2
+2a(x-1)+3a(x-1)(x+2); a2(2x-y)-a3(2x-y)
-3(2x-y); (x+y)(2x-1)(x+3)-(x+y)2(x+3)-(2x-1)2(x+y);
(a-1)3(a+2)(2a-1)-(a-
1)2(2a- 1)+(a+2)(a-1)(2a-1)2; -3n(n-2)3
-4n(n+2)(n +1) + (n+2)(n+ 1)2.
Lezione del 28/2/2001
Ricordare che...
- Qualsiasi equazione di 1°
grado può essere scritta nella forma: ax+b=0; a e b
sono i termini noti: a è un termine moltiplicativo (può essere
anche chiamato coefficiente
della variabile x) e b è un termine additivo.
- Ad ogni forma ax+b può essere associata una
relazione del tipo y=ax+b.
- Vogliamo trovare una
relazione tra equazioni e punti su un piano. A questo
scopo bisogna considerare che ogni punto del piano può
essere riferito a una coppia di rette ortogonali fra loro
dette asse delle ascisse
(normalmente orizzontalr e si indica con x) e asse delle ordinate
(di solito verticale e indicato con y); tale sistema di assi definisce
il piano cartesiano.
- Ogni punto P sul piano è individuato
univocamente sul piano cartesiano da una coppia di numeri
detti coordinate del punto P. Ad esempio il punto P(3,7) determina un punto che dista 3
unità dall'asse verticale e 7 unità dall'asse
orizzontale (v. figura)
______________________ 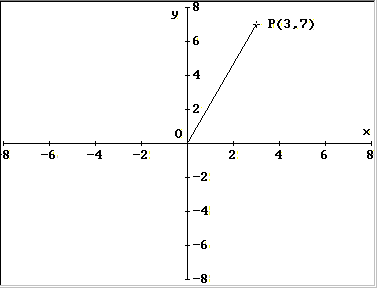
- Il punto di incontro degli
assi cartesiani viene chiamato origine
e ha coordinate P(0,0).
- La lunghezza del segmento OP è data, per il teorema di
Pitagora, da SQRT(32+72) dove SQRT indica l'operazione di
radice quadrata; in generale, la lunghezza del segmento
che unisce l'origine degli assi con un punto qualsiasi è
data da d=SQRT(x2+y2).
- La relazione algebrica y=ax+b definisce una retta sul piano
cartesiano; il termine a viene chiamato coefficiente
angolare della retta, mentre il termine b esprime la distanza del punto di
incontro della retta con l'asse y dall'asse orizzontale.
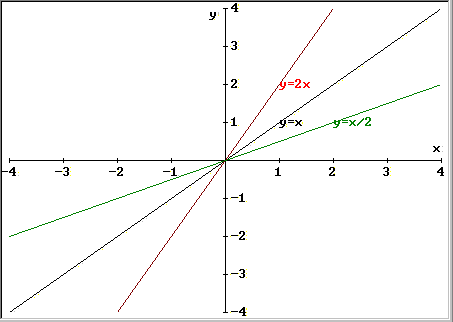
- Il significato del
coefficiente angolare può essere chiarificato dalla
seguente figura che mostra il grafico delle tre rette: y=x, y=2x, y=x/2;
si può osservare che, maggiore è l'entità del
coefficiente angolare maggiore sarà l'inclinazione della
retta rispetto l'asse x.
___________________
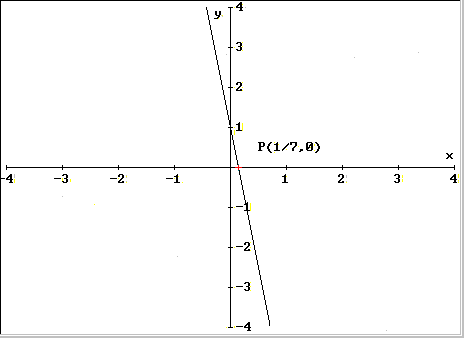
- E' facile rendersi conto
che la soluzione dell'equazione ax+b=0 associata alla retta y=ax+b rappresenta il punto in cui la
retta stessa incontra l'asse delle ascisse (definito
anche come la retta y=0);
ad esempio, la 1a equazione tra gli esercizi del
21/2/2001, effettuando gli opportuni passaggi, può
essere scritta -7x+1=0; la retta associata è, dunque, y=-7x+1; disegnando la retta (v. figura)
possiamo vedere che questa incontra l'asse x nel punto x=1/7 che è, appunto, la soluzione
dell'equazione -7x+1=0.
__________________
- Possiamo effettuare anche
il procedimento opposto: date le coordinate di due punti P1(x1,y1)
e P2(x2,y2) è possibile scrivere
l'equazione della retta passante per essi; infatti il
coefficiente angolare può essere calcolato tramite la
seguente relazione: a=(y2-y1)/(x2-x1) (provare a dimostrarla anche
solo intuitivamente). L'equazione completa sarà: y=x(y2-y1)/(x2-x1)+y0; il termine y0 rappresenta la distanza tra il
punto di incontro della retta con l'asse y (di equazione x=0) e l'asse x e si calcola tenendo conto che y0 è anche la lunghezza del
segmento verticale che unisce la retta di cui stiamo
cercando l'equazione e quella, parallela a quest'ultima,
che, con uguale coefficiente angolare, passa per
l'origine; la lunghezza di tale segmento verticale è
data dalla differenza tra l'ordinata y1 e, quella analoga, x1(y2-y1)/(x2-x1), relativa alla retta passante
per l'origine, cioè:y0=y1-x1(y2-y1)/(x2-x1); in figura è mostrata la retta
passante per i punti P1(1,3) e P2(4,5).
___________________
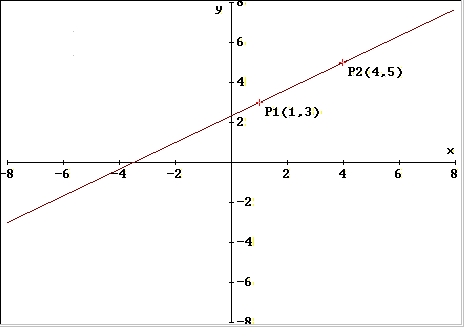
- Un insieme di 2 equazioni
in cui compaiano le stesse due incognite (ad es. x e y) soddisfatte contemporaneamente dagli
stessi valori è un sistema di equazioni
a 2 incognite; i due valori che soddisfano entrambe le
equazioni sono le soluzioni del sistema. Tale
definizione può essere generalizzata al caso in cui le
equazioni e le incognite siano n (n qualsiasi): in tal caso parliamo di sistema
di n equazioni a n incognite.
- Il metodo più semplice di
risoluzione è quello di sostituzione che
consiste nel risolvere una delle due equazioni rispetto
una delle incognite e sostituire l'espressione ottenuta
al posto della stessa incognita nell'altra equazione. Ad
es., dato il sistema {y+1=2x; y-2=3x, possiamo scrivere la 1a
equazione come y=2x-1
e sostituire l'espressione a destra del segno = al posto della y nella 2a equazione ottenendo,
così, l'equazione 2x-1-2=3x che, con le opportune semplificazioni,
diventa x=-3;
la y si trova sostituendo la x trovata precedentemente in una
della due equazioni, ad es. la prima, ottenendo y+1=2(-3) ovvero y=-7.
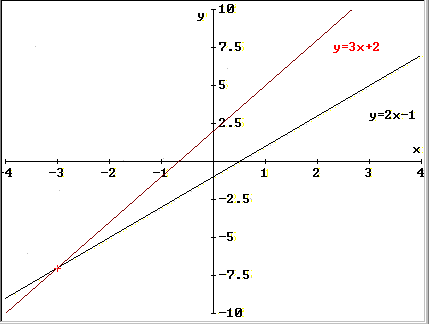
- Anche i sistemi di
equazioni hanno un preciso significato geometrico;
innanzitutto, le due equazioni determinano altrettante
rette (v. figura): le soluzioni del sistema sono le
coordinate del punto in cui si incontrano (come ci si
può rendere conto osservando la figura).
_____________________
Esercizi
Equazioni di 1° grado e
rette sul piano cartesiano
Provare a tracciare le rette
relative ad alcune delle equazioni dagli esercizi del 21/2/2001
verificando graficamente la correttezza delle souzioni (provare
anche una di quelle impossibili).
Sistemi di 2 equazioni
con 2 incognite
 2x-y=4
2x-y=4
 x+3y=9
x+3y=9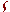 x+y=2
x+y=2
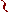 -x+2y=-17
-x+2y=-17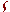 4x+y=-8
4x+y=-8
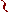 -2x+y=10
-2x+y=10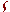 2x+y=5
2x+y=5
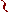 x-3y=-1
x-3y=-1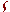 3x+5y=1
3x+5y=1
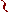 4x+y=7
4x+y=7 4x+3y=11
4x+3y=11
 2x+y=4
2x+y=4 3x+1=4y
3x+1=4y
 6x+2y-3=0
6x+2y-3=0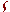 3x-4y=6
3x-4y=6
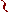 3x-y=3
3x-y=3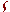 2x-y=3
2x-y=3
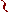 4x+y/2=1
4x+y/2=1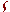 (4x-y)/6 +
x/4=1
(4x-y)/6 +
x/4=1
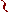 x+2y=12
x+2y=12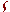 3x+2y=4
3x+2y=4
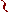 2y-3(x+3)/2=-5
2y-3(x+3)/2=-5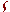 x+2y=2(2x-y+5)
x+2y=2(2x-y+5)
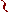 2-3x=y-1+2(x+6)
2-3x=y-1+2(x+6)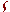 3x-5=2(y+1)-8
3x-5=2(y+1)-8
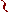 2(x-1)=3(1-2y)+9
2(x-1)=3(1-2y)+9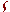 -[x-3(y-1)]+2x=3
-[x-3(y-1)]+2x=3
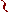 2(3x-y)+3(1-x)=-12
2(3x-y)+3(1-x)=-12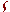 x-2[y-(x+1)]=12
x-2[y-(x+1)]=12
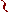 3x-2(y+3)=4
3x-2(y+3)=4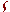 3x-2(y+1)=x+2(x-y)
3x-2(y+1)=x+2(x-y)
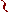 x+4y=0
x+4y=0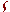 -2x+y=3
-2x+y=3
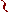 3y+x2=(3+x)2
3y+x2=(3+x)2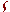 x/2-y=3
x/2-y=3
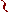 x+y/3=11/3
x+y/3=11/3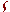 3y-2x=0
3y-2x=0
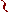 2x/3-y/2=1/6
2x/3-y/2=1/6 (y+1)/3+x/2=4
(y+1)/3+x/2=4
 1/2-(x+y)/6=2x/3-y/3
1/2-(x+y)/6=2x/3-y/3
Sistemi di equazioni e
intersezioni fra rette
Per alcuni dei sistemi dati
nell'esercizio precedente, tracciare le relative rette e
verificare graficamente le soluzioni trovate.
Lezione del 7/3/2001
Ricordare che...
- Qualsiasi equazione di 2°
grado può essere scritta nella forma ax2+bx+c=0, dove a è il coefficiente del termine
di 2° grado, b il
coefficiente del termine di 1° grado e c è il termine noto.
- Per trovare un metodo
generale di risoluzione basta trovare un modo per
esprimere la generica equazione di 2° grado in un quadrato
di un binomio. Ad es. ax2+bx+c=0, può diventare, moltiplicando
tutti i termini per 4a, 4a2x2+4abx+4ac=0; se portiamo il termine 4ac a secondo membro e addizioniamo b2 ad ambo i membri (operazione che
lascia comunque inalterata la validità della relazione
di uguaglianza), otterremo l'equazione 4a2x2+4abx+b2=b2-4ac; è facile rendersi conto che
l'espressione a primo membro è lo sviluppo del quadrato
del binomio 2ax+b
e che, pertanto, possiamo scrivere (2ax+b)2=b2-4ac; effettuando le opportune
manipolazioni otterremo, finalmente, la formula generale
di risoluzione che, come si vede, individua 2 soluzioni
_______________________________________
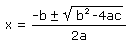
- Come per le equazioni di
1° grado, effettuiamo un collegamento tra Algebra e
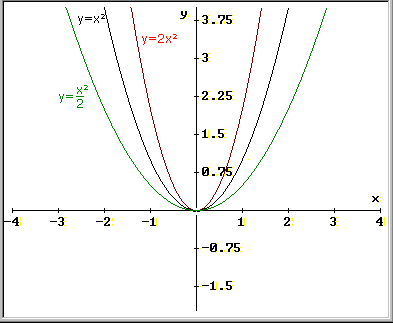
Geometria: una relazione di 2° grado individua una curva
detta parabola di equazione y=ax2+bx+c; nella figura sottostante
possiamo vedere le parabole di equazioni y=x2, y=2x2, y=x2/2 (il coefficiente del termine di
2° grado ha un significato analogo al coefficiente
angolare della retta)
______________________
- La generica parabola, y=ax2+bx+c, può essere disegnata fissando
sugli assi cartesiani i punti di incontro con l'asse x (le soluzioni dell'equazione) e
il punto di incontro con l'asse y (che si ottiene ponendo x=0) e ricordando che si tratta di
una curva simmetrica rispetto un asse che passa
per il suo punto di minimo (o di massimo);
quest'ultima affermazione ci porta a dedurre che il punto
centrale della parabola si ottiene conoscendo le
soluzioni dell'equazione associata...
- Se l'equazione non ammette
soluzioni numeriche semplici (ad es. se b2-4ac<0) la parabola non incontrerà
l'asse x.
- In generale un polinomio
di grado n in x è un'espressione in cui
compaiono un certo numero di termini contenenti la
variabile x
elevata ad una potenza non maggiore di n.
- Una disequazione
è una relazione in cui non si cerca un unico valore (o
un numero finito) che la soddisfi, ma un'infinità di
valori che la soddisfano e un'infinità di valori che,
eventualmente, non la soddisfano. Normalmente si cercano
i valori per cui una certa espressione è maggiore (o
minore) di un'altra.
- Una disequazione si risolve
in maniera analoga a quella in cui si risolve
un'equazione; ad es., 2x-1<0, portando i termini noti a secondo membro
con le ben note regole, diventa x<1/2 che equivale a dire che la
relazione è soddisfatta per tutti i valori della x minori di 1/2. Vale inoltre la regola che,
invertendo i segni ad ambo i membri, occorre cambiare il
verso della diseguaglianza per mantenere inalterata la
validità della relazione; ad es., -a<-b può essere cambiata in a>b.
Esercizi
- Equazioni di 2° grado
- x2-x-6=0
- x2-x-20=0
- x2-7x+10=0
- x2-8x+18=0
- x2-2x-35=0
- x2+2x-35=0
- x2+2x-8=0
- x2+x-6=0
- x2-4x+4=0
- 2x2+3x-20=0
- x2-9x-22=0
- 8x2+10x-7=0
- x2-x+1=0
- 6x2-5x-6=0
- 6x2+13x+6=0
- 4x2-12x+9=0
- 9x2+6x+1=0
- 3x2-2x+8=0
- (1/9)x2+(2/3)x+1=0
- 3x2-5x-12=0
- Parabole ed equazioni
di 2° grado
Disegnare le parabole relative
ad alcune delle equazioni precedenti ricordando che per far
questo basta trovare i punti di intersezione della curva con
l'asse x e quello di intersezione con l'asse y.
- Disequazioni di 1°
grado (provare a risolverle anche se non sono state
trattate nelll'ultima lezione)
- 12-1<1+2(x+4)
- 3+4(1+x)-(1+3x)>-2
- 3(x-1)-2<5x+1
- 4(2x-1)-3(1-2x)>5
- (1/3)x-(x/2-2)>(5-x)/6+1
- 3+2(x-1)>7+5(x-2)
- 8(5-x)+3(x-5)>0
- 9(20-5x)+27>8(5x-6)
Speditemi le
soluzioni di questi esercizi via e-mail (quando ciò è possibile) in modo che possa
cominciare a verifcarle prima della prossima lezione.
Lezione del 14/3/2001
Insiemi e
numeri
Insiemi
| Diagrammi
di Venn |
Elementi
di un insieme |
 |
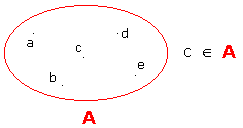 |
A e B
sono insiemi, cioè aggregati primitivi di
oggetti di qualsiasi natura. Il simbolo  sta per appartiene a:
nella figura, infatti, c è un elemento di A.
sta per appartiene a:
nella figura, infatti, c è un elemento di A.
Operazioni
fra insiemi
| Unione |
Intersezione |
Inclusione |
 |
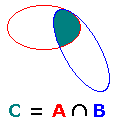 |
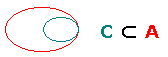 |
Nel primo caso (Unione)
l'insieme C è costituito dagli elementi di A
e dagli elementi di B. Nel secondo caso (Intersezione)
l'insieme C è formato dagli elementi comuni ad A
e B. Nel terzo, C è contenuto
in A e, quindi, è costituito da alcuni elementi
di A; C viene anche chiamato sottoinsieme
di A.
Alcune
definizioni
| Insieme
vuoto |
Applicazione
fra insiemi |
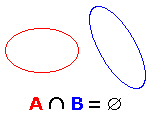 |
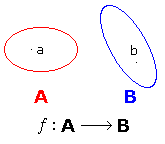 |
Un insieme che non ha elementi
viene definito come insieme vuoto; ad esempio
l'interserzione di due insiemi che non hanno elementi in comune
è un insieme vuoto. Esiste un'applicazione ƒ fra gli insiemi A e B
quando è definita una legge che associa un elemento a  A ad un
elemento b
A ad un
elemento b  B
B
Quantificatori
Definizione
esplicita di insiemi
| Per
elencazione |
Per
proprietà |
| A =
{Cinzia, Cristiano, David, Tiziana} B = {1, 2, 3, 4, 5, 6}
|
A = {x:
x è studente del corso di Matematica al Conservatorio} B = {x: x  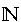 ; x < 7} ; x < 7}
|
Insiemi
numerici
Naturali
|
Interi
|
Razionali
|
x  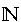
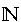 = {x:
x=1,2,3,...} = {x:
x=1,2,3,...}
|
x  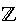
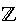 = {x:
x=...,-2,-1,0,1,2,3,...} = {x:
x=...,-2,-1,0,1,2,3,...}
|
x  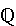
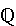 = {x: x=p/q; p,q = {x: x=p/q; p,q 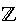 } }
|
Irrazionali
|
Reali
|
Complessi
|
x  I I
I = {x: x 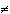 p/q; x p/q; x 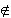 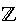 } }
|
x  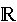
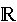 = = 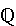  I I
|
x  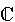
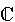 = {x: x = a +
jb; a,b = {x: x = a +
jb; a,b  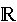 ; j2 =
-1} ; j2 =
-1}
|
E' ovvio che 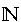
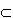
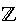
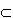
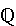
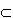
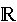
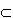
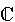
Intervalli
Aperto
|
Chiuso
|
Aperto-chiuso
|
Chiuso-aperto
|
| A = (a,
b) A = {x: x  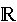 ; a < x < b} ; a < x < b}
|
A = [a,
b] A = {x: x  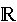 ; a £ x £ b} ; a £ x £ b}
|
A =
(a, b]
A = {x: x
 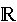 ; a < x £ b} ; a < x £ b}
|
A =
[a, b)
A = {x: x
 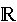 ; a £ x < b} ; a £ x < b}
|
a,b 
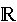 ; ad esempio 3
; ad esempio 3  (2, 4]; 2
(2, 4]; 2 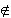 (2, 4]
(2, 4]
Intervalli
e geometria
L'insieme dei numeri reali (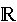 ) può essere messo in
relazione con una retta; un numero reale x
) può essere messo in
relazione con una retta; un numero reale x 
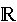 è rappresentato con un punto sulla retta
è rappresentato con un punto sulla retta
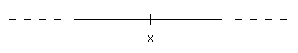
Un intervallo è analogo a un
segmento; un punto x  [a,b] è un punto interno al segmento
[a,b] è un punto interno al segmento
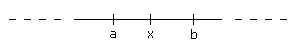
L'insieme dei numeri complessi (a + jb 
 ) è
rappresentabile con un piano in cui sia definito un sistema di
assi cartesiani: sulle ascisse troviamo la parte reale
(a, cioè la parte non moltiplicata per
l'unità immaginaria j) mentre sulle ordinate troviamo la parte
immaginaria (b, ovvero il fattore che moltiplica l'unità
immaginaria j); un numero complesso x
) è
rappresentabile con un piano in cui sia definito un sistema di
assi cartesiani: sulle ascisse troviamo la parte reale
(a, cioè la parte non moltiplicata per
l'unità immaginaria j) mentre sulle ordinate troviamo la parte
immaginaria (b, ovvero il fattore che moltiplica l'unità
immaginaria j); un numero complesso x 
 , dunque, è rappresentato con un punto
sul piano
, dunque, è rappresentato con un punto
sul piano
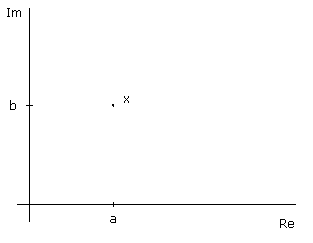
Pagina iniziale ____________ Informatica e Telematica____________ Programma ____________ Bibliografia
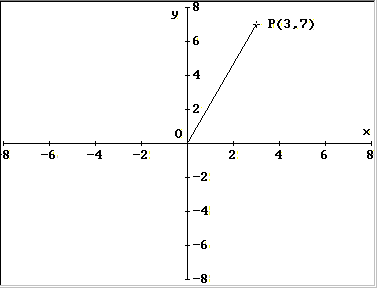
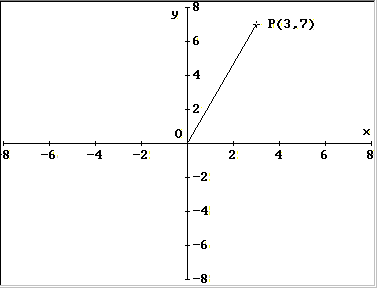


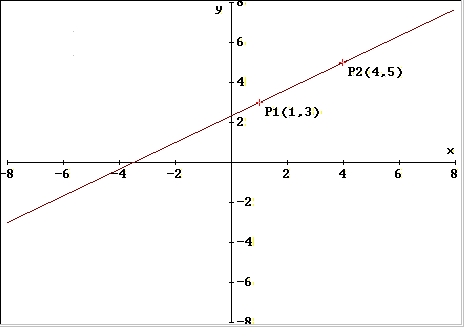

![]()



![]() sta per appartiene a:
nella figura, infatti, c è un elemento di A.
sta per appartiene a:
nella figura, infatti, c è un elemento di A.
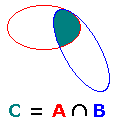

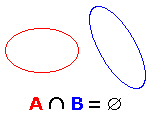

![]() A ad un
elemento b
A ad un
elemento b ![]() B
B![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() ; ad esempio 3
; ad esempio 3 ![]() (2, 4]; 2
(2, 4]; 2 ![]() (2, 4]
(2, 4]![]() ) può essere messo in
relazione con una retta; un numero reale x
) può essere messo in
relazione con una retta; un numero reale x ![]()
![]() è rappresentato con un punto sulla retta
è rappresentato con un punto sulla retta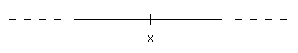
![]() [a,b] è un punto interno al segmento
[a,b] è un punto interno al segmento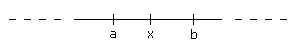
![]()
![]() ) è
rappresentabile con un piano in cui sia definito un sistema di
assi cartesiani: sulle ascisse troviamo la parte reale
(a, cioè la parte non moltiplicata per
l'unità immaginaria j) mentre sulle ordinate troviamo la parte
immaginaria (b, ovvero il fattore che moltiplica l'unità
immaginaria j); un numero complesso x
) è
rappresentabile con un piano in cui sia definito un sistema di
assi cartesiani: sulle ascisse troviamo la parte reale
(a, cioè la parte non moltiplicata per
l'unità immaginaria j) mentre sulle ordinate troviamo la parte
immaginaria (b, ovvero il fattore che moltiplica l'unità
immaginaria j); un numero complesso x ![]()
![]() , dunque, è rappresentato con un punto
sul piano
, dunque, è rappresentato con un punto
sul piano