Lezione del 2/5/2001
La successione è stata già definita come un'applicazione
dove D 
, C 
, n 
D . La f(n)
è, quindi, un'enumerazione di elementi numerici reali;
l'argomento n può essere visto come un indice e quindi una
successione è un insieme di elementi individuati univocamente da
un indice. Ad esempio, {x(n)} = {1,2,4,8,16,32,64} è una successione di 6 elementi dove x(0)=1, x(1)=2, x(2)=4, etc.; la stessa successione, definita
esplicitando direttamente i suoi termini, può essere definita
evidenziando il legame funzionale tra la x e la
n, ovvero x(n)=2n, n=0,1,...,6. Nella letteratura scientifica una successione
può essere anche indicata con {xn} il che
evidenzia la natura enumerativa della successione; l'altra
notazione, invece, rivela la sua natura funzionale; si possono
usare indifferentemente le due notazioni.
Lo studio delle successioni è importante per il musicista "elettronico" perché l'analisi e la sintesi di segnali campionati viene effettuata con il calcolatore usando metodi matematici molto potenti; l'insieme di tali metodi è il Digital Signal Processing e le entità matematiche che trattano sono successioni. Infatti, se campioniamo un segnale (alla corretta frequenza di campionamento) e conserviamo i valori numerici ottenuti su un supporto di memoria, viene, per così dire, persa la dipendenza dal tempo del segnale; ciò che abbiamo è solo una successione di numeri.
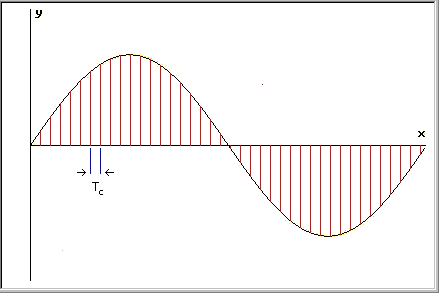
Esempio di sinusoide campionata
Data una successione {xn} di N termini è possibile costruire nuove successioni derivate formate dai suoi elementi scelti in base a diversi criteri.
Le più semplici modalità di scelta sono: le disposizioni, le permutazioni, le combinazioni
Nella letteratuira scientifica spesso vengono usati gli stessi termini per indicare oggetti matematici leggermente diversi di volta in volta; l'unico che non presenta ambiguità e il termine combinazione
Nella matematica discreta (è il caso delle successioni e del calcolo combinatorio) è importante conoscere sia il numero di possibili successioni derivate secondo un certo criterio che il metodo per costruirle. Il secondo caso è più di dominio dell'informatica che della matematica.
Sono le successioni
{yk} (yk{xn} k=0,1,...,K) formate da elementi di {xn} scelti tenendo conto dell'ordine in cui
compaiono e con ripetizioni.
Il numero di disposizioni di K elementi da un insieme di N è dato da NK; infatti, per induzione, se K=1 abbiamo N possibili scelte, se K=2 abbiamo N possibili scelte di N possibili scelte (quindi N*N) e in generale N*N*....*N per K volte.
Ad esempio, se {xn}={0,1} cioè l'insieme delle 2 cifre binarie (i bit), vogliamo sapere quante configurazioni da K bit sono possibili: con 1 bit sono possibili 2 configurazioni {yk}={0,1}, con 2 bit ne sono possibili il doppio perché per ogni configurazione da 1 bit ce ne sono 2 (00 e 10, 01 e 11) e così via raddoppiando ogni volta che viene aggiunto un bit cioè 2*2*...*2 per K volte ovvero 2K.
Il numero di configurazioni possibili si riduce se nella scelta degli elementi di {xn} per formare {yk} non ammettiamo ripetizioni.
In questo caso K £ N e le successioni derivate vengono chiamate k-permutazioni. Se K=N le successioni derivate sono chiamate semplicemente permutazioni.
Per conoscere il numero di k-permutazioni di N elementi ragioniamo in maniera analoga a quanto fatto nel punto precedente: in una 1-perrmutazione abbiamo N possibili scelte; in una 2-permutazione abbiamo N-1 possibili scelte per ognuna delle N scelte del caso 1 e, pertanto, N(N-1) scelte e così via scalando di 1 per ogni elemento aggiunto; in generale ci saranno N(N-1)(N-2)...(N-K+1) k-permutazioni.
Dato che una permutazione è una N-permutazione avremo N(N-1)(N-2)...(2)(1) permutazioni.
L'ultimo risultato si indica in maniera più compatta con N! e viene detto N fattoriale. Pertanto il numero di k-permutazioni possibili sono N!/(N-K)!
Il numero di configurazioni possibili si riduce ulteriormente se nella scelta degli elementi di {xn} per formare {yk} imponiamo anche la condizione che l'ordine in cui compaiono gli elementi di uno stesso sottoinsieme non ha importanza; ad esempio, se {xn}={a1,a2,a3,a4,a5,a6}, le successioni derivate {a2,a3} e {a3,a2} sono considerate equivalenti e, quindi, come se fosse un unico insieme formato dagli elementi a2 e a3.
In questo caso K £ N e le successioni derivate vengono chiamate combinazioni.
Da quanto detto, possiamo dedurre facilmente il numero di combinazioni di K elementi da un insieme di N; infatti, poiché non conta l'ordine con cui vengono scelti i K elementi, si prenderà soltanto una delle K! permutazioni di termini della successione derivata. Siccome le k-permutazioni (cioè tutte le sottosuccessioni) {yk} di {xn} sono N!/(N-K)! ne segue che le combinazioni sono N!/[K!(N-K)!].
L'ultima formula viene indicata
col simbolo 
chiamato anche coefficiente binomiale.
- Disposizioni
- Permutazioni e k-permutazioni
- Combinazioni
- In generale
Pagina iniziale ____________ Informatica e Telematica____________ Programma ____________ Bibliografia