Lezione del 23/5/2001
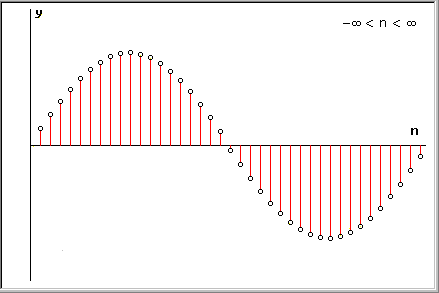
Una successione {x(n)} è, di norma, definita per tutti gli indici n interi. Nella figura è mostrato il grafico di una successione (in particolare di x(n) = sen(wn)).

Il "pallino" bianco alla sommità di ogni linea rappresenta il valore del campione x(n). La successione è formata da tutti i "pallini"; negli altri punti la successione non è definita.
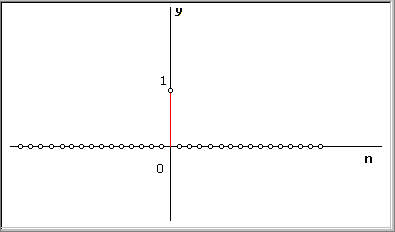
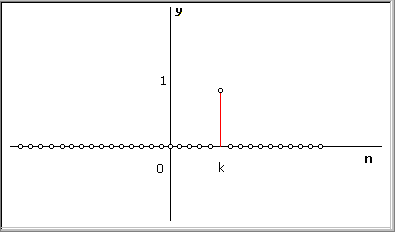
Di seguito sono mostrate alcune successioni particolari. La prima è l'impulso unitario ed è così definito
 |
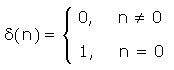 |
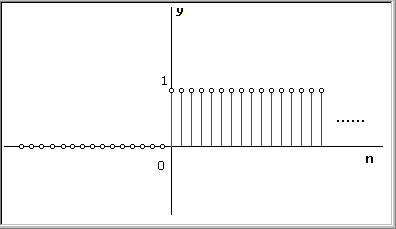
Un'altra importante successione è il gradino unitario
 |
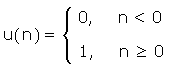 |
| Il gradino è legato all'impulso dalla formula | 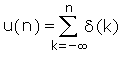 |
| mentre l'impulso può essere scritto | d(n) = u(n) - u(n-1) |
Quella mostrata sotto è la successione esponenziale an.
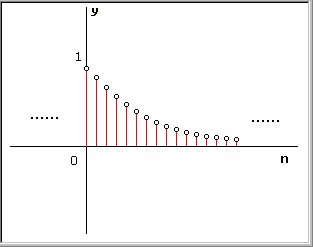 |
a |
Una successione x(n) si dice ritardata di un fattore k e si indica con x(n - k) se tutta la successione è traslata a destra (se k>0) di k campioni. Ad esempio, l'impulso ritardato
 |
x(n)
= d(n - k) (in questo caso k = 5) |
Una successione qualsiasi può essere rappresentata come somma di impulsi unitari scalati (moltiplicati per il valore del k-mo campione della successione) e ritardati:
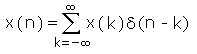 |
Ad esempio |
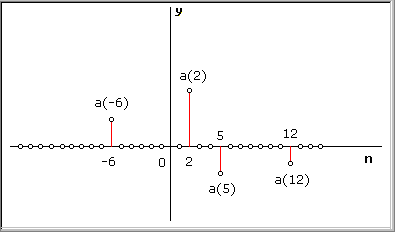 |
a(n) = |
Definizione ricorsiva di una successione (equazioni alle differenze)
Una successione può essere definita ponendo in relazione il suo n-mo termine con i termini precedenti. Ad esempio, possiamo scrivere y(n) = a1y(n-1)+a2y(n-2)+...+aky(n-k). La precedente viene chiamata anche relazione di ricorrenza. Una formula ricorsiva come la precedente può essere usata solo definendo k condizioni iniziali.
Si definisce differenza prima la quantità Dy(n) = y(n) - y(n-1). La differenza seconda D2y(n) sarà Dy(n) - Dy(n-1) = y(n) - 2y(n-1) + y(n-2). Allo stesso modo si può definire qualsiasi ordine di differenza Dky(n).
E' possibile generalizzare la relazione di ricorrenza di una successione esprimendola come equazione alle differenze (omogenea) ckDky(n)+...+c2D2y(n)+c1Dy(n)+c0y(n) = 0.
Come si vedrà nella trattazione dell'elaborazione numerica dei segnali, un'equazione alle differenze definisce un filtro digitale.
La successione definita con la relazione ricorsiva j(n) = j(n-1) + j(n-2) con le condizioni iniziali j(1) = j(0) = 1, n=2,3,.... , viene chiamata successione di Fibonacci. Tale successione gode di molte interessanti proprietà.
| Si può calcolare il termine
n-mo della successione con la formula di Binet (indicata
qui a destra). Si può dimostrare che j(n) / j(n-1) » a. La relazione precedente indica che il rapporto tra due numeri di Fibonacci consecutivi si avvicina sempre più ad a al crescere di n. |
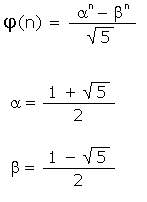 |
Applicazioni geometriche della successione di Fibonacci
Sia dato un segmento AB suddiviso nella seguente maniera
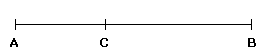
La costruzione è tale che il rapporto tra le lunghezze dei segmenti AB e CB è uguale a quello tra CB e AC. Il segmento CB è detto medio proporzionale tra AB e AC.
Senza perdere in generalità si assegna ad AB la lunghezza 1 e si indica con x la lunghezza del segmento CB. Pertanto sarà 1/x = x/(1 - x). Risolvendo l'equazione di 2° grado che si ottiene manipolando la precedente formula avremo che il rapporto 1/x tra le misure di AB e CB sarà uguale ad a (v. paragrafo precedente).
La suddivisione del segmento (o di qualsiasi entità ad esso correlata) con tali proprietà viene chiamata sezione aurea.
- Dimostrare l'espressione della differenza seconda
- Calcolare la formula generale per la differenza k-ma
- Dimostrare che un'equazione alle differenze omogenea è equivalente a una relazione di ricorrenza
- Dimostrare che il rapporto di sezione aurea è uguale al numero a » j(n)/j(n-1)
Pagina iniziale ____________ Informatica e Telematica____________ Programma ____________ Bibliografia