Lezione del 13/6/2001
Esercizi di riepilogo
-
Determinare il dominio di esistenza delle seguenti funzioni
- y = x / (x
- 1)
- y =
sqrt(x-2) / sqrt(x2+2)
- y = (x2+3)
/ (x2+4)
- y = e-x
/ (x2+1)
- y = ln(x+1)
- y = ln(x2+5)
- y = ln[x2
/ (x+3)]
- y =
ln[sqrt(x2+1)]
- y = ln(x3+3)
- y =
sqrt(ln(x-1))
- Sui
logaritmi
- Un filtro
passa-basso passivo ha un fattore di attenuazione pari a 6 dB / ottava (l'ottava è
l'intervallo che si ottiene raddoppiando la frequenza di
una nota): cosa significa quest'affermazione?
- E quali
conclusioni possiamo trarre dal fatto che un filtro
passa-basso ha un fattore di attenuazione di 48 dB / ottava?
- Si è detto
che l'intervallo di ottava corrisponde a un raddopiamento
della frequenza; la maggior parte delle scale musicali in
uso nelle culture più disparate si basa su divisione
dell'ottava secondo criteri diversi; uno di questi è la
trasposizione delle frequenze armoniche (cioè le
frequenze multiple intere della fondamentale che è
quella relativa all'altezza che si percepisce); ad
esempio l'intervallo di 12a corrisponde all'intervallo
tra la fondamentale e la 3a armonica (cioè a un rapporto
uguale a 3 fra l'armonica e la fondamentale): per
ottenere l'intervallo di 5a basta trasporre di un'ottava
tale intervallo ottenendo così un rapporto di 3/2. La
scala temperata occidentale (a intervalli equalizzati) si
basa su una divisione dell'ottava tale che l'intervallo
di base (il semitono) è sempre uguale in qualsiasi punto
si faccia iniziare la scala; il rapporto tra l'altezza di
una nota e del semitono successivo è dato da
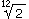 . Per poter
usare i rapporti tra altezze in maniera additiva si suole
esprimerli tramite i logaritmi in base 2 in modo che
tutti gli intervalli siano espressi con un numero
compreso tra 0 e 1. Dimostrare che la quinta naturale
(rapporto 3/2) è praticamente identica alla quinta
temperata.
. Per poter
usare i rapporti tra altezze in maniera additiva si suole
esprimerli tramite i logaritmi in base 2 in modo che
tutti gli intervalli siano espressi con un numero
compreso tra 0 e 1. Dimostrare che la quinta naturale
(rapporto 3/2) è praticamente identica alla quinta
temperata.
- Realizzare
un programma Csound che permetta di ascoltare le prime 16
armoniche di un suono fondamentale a 261 Hz.
- Dallo
stesso programma del punto precedente ricavare un
programma che permetta di verificare acusticamente sia
gli intervalli naturali che quelli temperati.
- Rappresentare in
maniera polare i seguenti numeri complessi
- 1 + j1
- 2 + j3
- 1 - j2
- 4 + j5
- 3 - j7
- Dimostrare la seguente
uguaglianza (Formula di De Moivre)
- [r(cosj + jsenj)]n = rn[cos(nj) + jsen(nj)]
- Disegnare gli spettri
delle seguenti modulazioni ad anello
- fp = 300;
f1 = 250, a1 = 1; f2 = 280, a2 = 2
- fp = 1500;
f1 = 1400, a1 = 1.5; f2 = 1200, a2 = 1
- fp = 1000;
f1 = 400, a1 = 1; f2 = 800, a2 = 1/2; f3 = 1200, a3 = 1/3
- fp = 700;
f1 = 100, a1 = 1; f2 = 200, a2 = 1/4; f3 = 300, a3 = 1/9
- Realizzare
un programma Csound per ascoltare i risultati sonori
delle precedenti modulazioni
- Verificare le seguenti
uguaglianze
- 4cos3x
- 3cosx = cos3x
- 8cos4x
- 8cos2x + 1 = cos4x
- 16cos5x
- 20cos3x + 5cosx = cos5x
- 32cos6x
- 48cos4x + 18cos2x - 1 = cos6x
- 64cos7x
- 112cos5x + 56cos3x - 7x = cos7x
- cosnx = cosnx
-
 cosn-2x
(1-cos2x) +
cosn-2x
(1-cos2x) +  cosn-4x (1-cos2x)2
+
cosn-4x (1-cos2x)2
+  cosn-6x
(1-cos2x)3 + ....
cosn-6x
(1-cos2x)3 + ....
- Dimostrare le seguenti
affermazioni
- I primi membri delle
uguaglianze da 1 a 5 del gruppo precedente di esercizi
sono state ottenute applicando la formula generale al
secondo membro dell'espressione n° 6
- La formula generale del n°
6 del gruppo precedente si può ricavare dalla seguente
relazione di ricorrenza: Tn(y) = 2yTn-1(y)
- Tn-2(y)
per n
= 2, 3, ... , dove y è una qualsiasi espressione o
funzione (nel gruppo precedente era y = cos(x)) e T0 = 1 e T1 = y.
nota: le Tn(y) sono anche chiamate polinomi di
ChebyChev e godono di importanti proprietà che saranno
chiare quando si studieranno i metodi di sintesi non lineari (waveshaping).
- Disposizioni,
permutazioni, combinazioni
- Quante parole italiane da 5
caratteri si possono costruire?
- Quante password di
6 caratteri sono possibili usando un insieme di simboli
comprendente le lettere maiuscole e minuscole, le cifre
numeriche e i segni di interpunzione.
- Quante sequenze di altezze
diatoniche di 5 note possono essere costruite in
un'ottava?
- Quante sono le sequenze
ritmiche (ad altezza fissa) in una misura di 3/4
ottenibili solo con crome e relative pause?
- Quanti sono gli anagrammi
della parola "BISCROMA" (anche privi di
significato)?
- In quante maniere è
possibile disporre (indipendentemente dal significato
armonico e dall'ottava) le note di un accordo di 5a
aumentata?
- Quante
"combinazioni" di 7 simboli diversi sono
possibili per una cassaforte dotata di un tastierino
numerico?
- Quante cinquine sono
possibili al gioco del Lotto?
- Quanti accordi di 3 suoni
(diversi) possono essere costruiti con le sole note di
una scala maggiore?
- Quante melodie (complete
dei valori di durata e pause fino alla croma esclusi
punti e gruppi irregolari) di 12 note si possono
realizzare usando una scala pentatonica
- Vettori
Dato un vettore qualsiasi v, dimostrare che
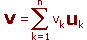
(sapendo che vk = vuk).
- Eseguire i seguenti
prodotti fra matrici
- Permutazioni a 2
dimensioni
Due quadrati latini distinti si
dicono ortogonali se il quadrato formato dalle
coppie di elementi corrispondenti dei 2 quadrati ha elementi
diversi; in questo caso, tali quadrati si dicono greco-latini.
Ad esempio:
| Quadrato 1
|
Quadrato 2
|
Quadrato
greco-latino
| (0,2) |
(1,1) |
(2,0) |
| (1,0) |
(2,2) |
(0,1) |
| (2,1) |
(0,0) |
(1,2) |
|
- Provare a costruire
quadrati greco-latini di ordine 4,5,6
- Successione di
Fibonacci
- Calcolare j(24) usando la formula di Binet
- Calcolare i limiti
delle seguenti successioni
- x(n) = n /
(n2 + 3)
- x(n) = (n2
+ n + 1) / (n + 1)
- x(n) = n!
- x(n) = an
/ n!
- sqrt(n) -
sqrt(n-1)
- Calcolare i limiti
delle seguenti funzioni
- f(x) = x /
(x2 + 2) per x tendente a -2
- f(x) = (x2
+ x + 1) / (x - 2) per x tendente a 2
- f(x) = x /
(x2 + 2) per x tendente a -2
- f(x) = ex
/ (x3 + 1) per x tendente a -1 e per x tendente a ¥
- f(x) =
sqrt(x) / sqrt(x3 + 1) per x tendente a ¥
- Tutte le
funzioni del 1° gruppo di esercizi (ricerca del dominio)
nei punti non appartenenti al dominio di esistenza
Pagina iniziale ____________ Informatica e Telematica____________ Programma ____________ Bibliografia
![]()