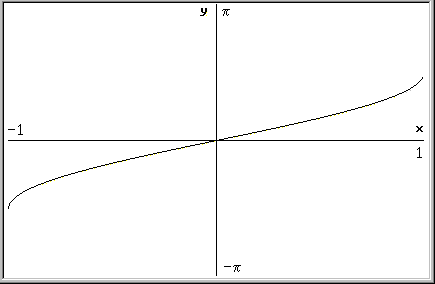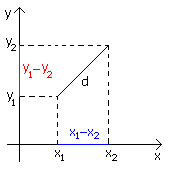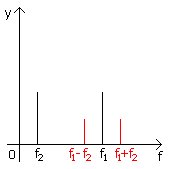Lezione del 4/4/2001
Trigonometria
>>
Funzioni goniometriche
inverse
| Arcoseno (arcsen(x)) |
Grafico di arcsen(x) |
L'arcoseno
è definito come funzione inversa del seno; pertanto,
quando scriviamo y = arcsen(x)
intendiamo dire che y è l'arco il
cui seno é x; ad esempio p/2 è l'arco
il cui seno è uguale a 1 (cioè: arcsen(1) = p/2)
|
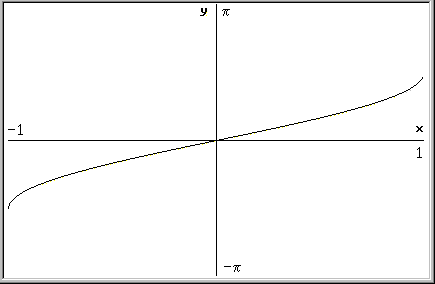 |
| Arcocoseno
(arccos(x)) |
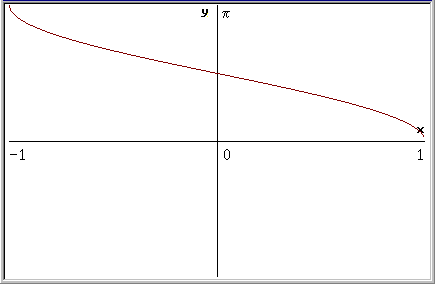
Grafico
di arccos(x) |
L'arcocoseno
è la funzione inversa del coseno; quindi y = arcsen(x) significa che y è l'arco il cui coseno é x; ad esempio p è
l'arco il cui coseno è uguale a -1 (cioè: arccos(-1) = p)
|
 |
| Arcotangente (arctg(x) o
atan(x)) |
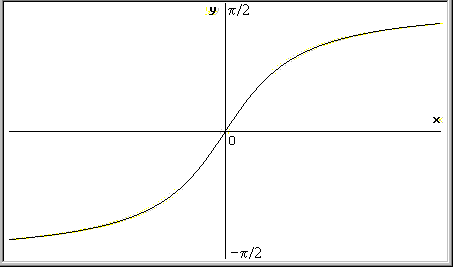
Grafico di arctg(x) |
L'arcotangente
è definito come funzione inversa della tangente;
pertanto, quando scriviamo y = arctg(x)
intendiamo dire che y è l'arco la
cui tangente é x; ad esempio p/4 è l'arco la cui tangente è uguale a 1 (cioè: arctg(1) = p/4)
|
 |
Possiamo precisare meglio,
adesso, il significato della fase in una rappresentazione grafica
di un punto sul piano in coordinate polari
| |
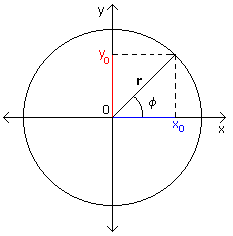
Coordinate
polari di un punto |
Modulo
r2
= x02 + y02
Fase
Dato
che:
x0
= r cos f
y0 = r sen f
y0/x0
= r sen f / r cos f = tg f
Pertanto
f = arctg(y0/x0)
|
 |
>>
Numeri complessi e trigonometria
| |
Rappresentazione
polare dei numeri complessi |
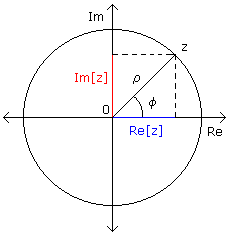 |
Dalla figura
accanto possiamo dedurre un rappresentazione alternativa
dei numeri complessi che sarà molto utile in seguito (ad
es. nell'analisi di Fourier). Se nel piano complesso
facciamo in modo che il punto (che rappresenta un numero
complesso z=Re[z]+jIm[z]) faccia parte di una circonferenza di
raggio r centrata
nell'origine degli assi, potremo esprimere le sue
coordinate in forma polare r = sqrt(Re[z]2 +
Im[z]2)
f = arctg(Im[z] / Re[z]) =
arg(z)
l'angolo f viene anche chiamato argomento;
poiché
Re[z] = rcosf
Im[z] = rsenf
ne consegue la
forma polare dei numeri complessi
z = r(cosf + jsenf)
|
>>
Formule di addizione di
archi e rappresentazione in quadratura di fase
| Distanza
tra due punti generici |
|
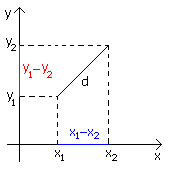 |
La
distanza tra due punti generici sul piano può essere
trovata dalla semplice relazione d2 =
(y2 - y1)2 + (x2
- x1)2
come risulta evidente
dalla figura a fianco.
|
| |
|
| Coseno
della differenza di archi |
|
|
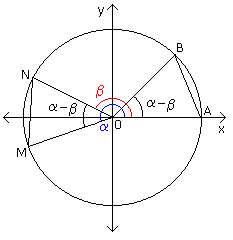
Dalla
costruzione geometrica mostrata a fianco, possiamo
ricavare le coordinate dei punti A, B, M, N
A = (1,0)
B = (cos(a-b), sen(a-b))
N = (cosb, senb)
M = (cosa, sena)
pertanto
poiché AB = MN
(cos(a-b) -1)2 + sen(a-b)2 =(cosa - cosb)2
+(sena - senb)2
da cui
2 - 2cos(a-b) = 2 - 2cosacosb + 2senasenb
ottenendo, così, le formule di
sottrazione degli archi per il coseno:
cos(a-b) = cosacosb + senasenb
|
| |
|
| Funzioni
pari e dispari |
|
|
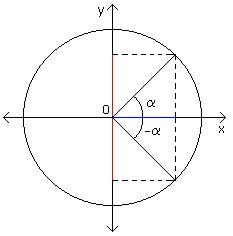
Una funzione f(x) si dice pari quando f(-x) = f(x) (cioè quando è simmetrica
rispetto l'asse y;
si dice dispari quando è antisimmetrica
rispetto l'asse y, cioè se f(-x) = -f(x).
Dalla figura si
vede che il seno è dispari e il coseno è pari, ovvero:
cos(-a) = cosa
sen(-a) = -sena
|
Da questa
figura si vede la simmetria del coseno rispetto l'asse y
|

|
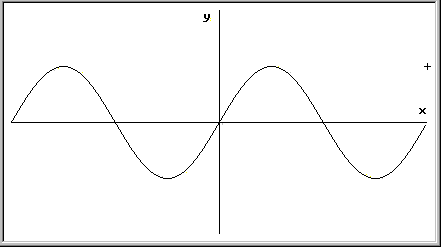
Qui, invece,
è evidente l'asimmetria del seno rispetto l'asse y
|
|
Invertendo il
segno di b otterremo facilmente le formule
di somma per il coseno
cos(a+b) = cosacosb - senasenb
Poiché cos x = sen(x+p/2) sarà anche sen x = cos(x-p/2) = cos(p/2-x) per la
parità del coseno; otterremo quindi le formule di somma
e sottrazione di archi per il seno
sen(a-b) = senacosb - senbcosa
sen(a+b) = senacosb + senbcosa
Infine, dalle
precedenti identità, possiamo ottenere facilmente le formule
di duplicazione degli archi per il seno e il coseno
sen2a = 2senacosa
cos2a = cos2a - sen2a = 1 - 2sen2a = 2cos2a - 1
Dalle
formule di somma possiamo ricavare un'espressione utile a
rappresentare un'onda sinusoidale di frequenza f =w/2p sfasata di un angolo f costante
y
= sen(wt + f) = senwtcosf + senfcoswt
poiché
è costante, possiamo scrivere A = senf, B = cosf, pertanto
sen(wt + f) = Acoswt + Bsenwt
Cioè
l'onda sinusoidale espressa come somma pesata di 2 componenti in quadratura
di fase
>>
Formule di bisezione
Dalla formula di
duplicazione per il coseno potremo scrivere
cos x = 1
- 2sen2(x/2)
cos x = 2cos2(x/2) -1
ottenendo le formule di bisezione
sen(x/2) =
sqrt([1-cos x)/2])
cos(x/2) =
sqrt([1+cos x)/2])
>>
Formule di prostaferesi e di Werner
Eseguendo le somme e
sottrazioni
sen(a+b) + sen(a-b) = 2senacosb
sen(a+b) - sen(a-b) = 2senbcosa
e sostituendo a = (p + q) / 2 e b = (p
- q) / 2, otterremo le formule
di prostaferesi per il seno (quelle per il coseno si
lasciano come esercizio)
sen p + sen q =
2sen[(p+q)/2]cos[(p-q)/2]
sen p - sen q = 2cos[(p+q)/2]sen[(p-q)/2]
Queste formule sono utili
per il calcolo delle frequenze relative ai battimenti
fra due onde sinusoidali
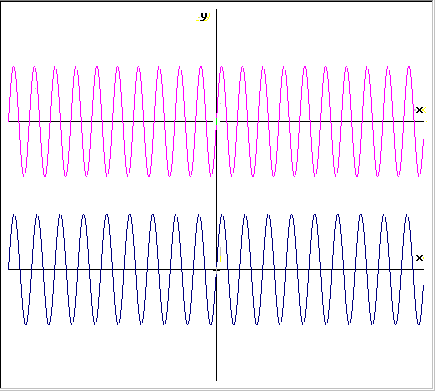 |
Se abbiamo due oscillazioni
sinusoidali y1
= senw1t
y2 = senw2t
di frequenze f1=w1/2p e f2=w2/2p
leggermente differenti
consideriamo la loro
sovrapposizione (somma)
y = y1
+ y2
|
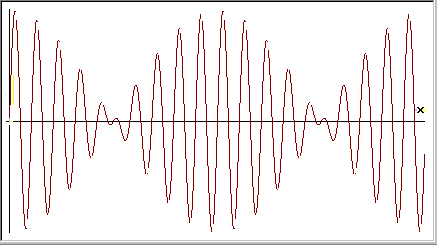 |
Otterremo il ben noto fenomeno
dei battimenti |
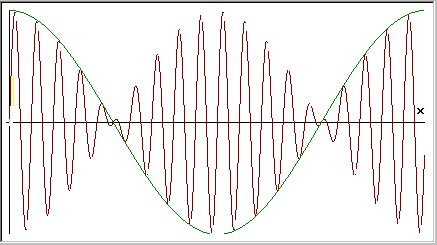 |
Per le formule di prostaferesi,
la forma d'onda risultante sarà composta da una
sinusoide di frequenza (f1
+ f2)/2
inviluppata
da una cosinusoide (in verde) di frequenza
(f1 - f2)/2 |
Direttamente dalle formule
di prostaferesi avremo le formule di Werner
sena cosb = [sen(a+b) + sen(a-b)]/2
le
altre due si lasciano come esercizio
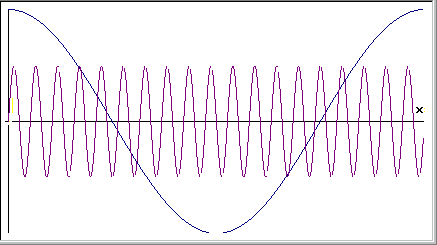 |
Le formule di Werner sono utili
per il calcolo delle componenti sinusoidali risultanti
dal prodotto fra due onde (la ben nota ring
modulation). Se moduliamo la sinusoide y1 = senw1t con la cosinusoide y2 = cosw2t avremo un onda y = y1y2 |
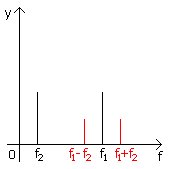
|
Lo spettro del
segnale risultante è mostrato nella figura a fianco ed
è stato ottenuto usando le formule di Werner. |
>>
Esercizi
- Dimostrare (geometricamente)
le seguenti identità
- sen 30° = 1/2 ; cos 30° =
sqrt(3)/2
- sen 45° = cos 45° =
sqrt(2)/2 ; tg 45° = 1
- sen 60° = sqrt(3)/2 ; cos
60° = 1/2
- Calcolare i seguenti
valori
- arcsen(-1)
- arcsen(-sqrt(2)/2)
- arccos(1)
- arctg(-1)
- arccos(0.5)
- Esprimere in
coordinate polari i seguenti punti rappresentandoli graficamente
in modulo e fase
- (1,2)
- (2,1)
- (3,3)
- (1.5,2.5)
- (0.5,2)
- Rappresentare in
maniera polare i seguenti numeri complessi
- 2 + j3
- 4 + j9
- 1 + j5
- 7 + j7
- 3 + j2
- Calcolare i seguenti
valori (usando le formule di somma e sottrazione e le
identità precedentemente dimostrate)
- sen 105° ;
cos 105°
- sen 75° ;
cos 75°
- sen 120° ;
cos 120°
- sen 150° ;
cos 150°
- Rappresentare in
quadratura di fase le seguenti oscillazioni
- 3sen(wt + p/4)
- 4sen(wt + p/6)
- cos(wt + p/3)
- 2sen(wt + p/4)
- 3cos(wt + p/2)
- Terminare le
dimostrazioni delle formule di bisezione (la tangente),
di prostaferesi e di Werner
- Disegnare il grafico
delle seguenti composizioni di onde sinusoidali (di cui
sono dati i parametri ampiezza, frequenza e fase)
- Amp.1 = 2,
freq.1 = 10, fase1 = 0; Amp.2 = 1, freq.2 = 11, fase2 = 0
- Amp.1 = 1,
freq.1 = 30, fase1 = 0; Amp.2 = 2, freq.2 = 29, fase2 = 0
- Amp.1 =
0.5, freq.1 = 15, fase1 = 0; Amp.2 = 1, freq.2 = 50,
fase2 = 90
- Disegnare lo spettro
delle seguenti modulazioni ad anello
- Amp.1 = 2,
freq.1 = 100, fase1 = 0; Amp.2 = 1, freq.2 = 150, fase2 =
90
- Amp.1 = 1,
freq.1 = 300, fase1 = 0; Amp.2 = 2, freq.2 = 200, fase2 =
90
- Amp.1 =
0.5, freq.1 = 150, fase1 = 0; Amp.2 = 1, freq.2 = 500,
fase2 = 0
Pagina iniziale ____________ Informatica e Telematica____________ Programma ____________ Bibliografia